Picto La Vague

Juillet  2025

La Vague n°86

BFS et SUS

Télécharger le numéro

Sommaire

✻

L’analyse de la normalité en Continued Process Verification

Les outils statistiques dits de Statistical Process Control (SPC) sont des incontournables dans la maitrise des procédés, notamment dans une démarche de Vérification Continue des Procédés (CPV). Ces outils ont pour objectif d’aider . démontrer que le procédé de fabrication est stable et qu’il présente une bonne capacité à générer des produits qui répondent aux spécifications attendues. Concrètement, il s’agit d’étudier la variabilité du procédé et du produit afin de caractériser et de discerner les causes de variabilité “spéciales” (c’est-à-dire liées à un événement non prévu ou à un défaut de mise sous contrôle) et les causes “communes” (liées à la variabilité naturelle du procédé dans son fonctionnement usuel).

Beaucoup de ces outils sont désormais démocratisés dans les logiciels de statistiques : cartes de contrôle, analyse de la capabilité, intervalles de tolérance ou de prédiction et autres outils dérivés des méthodes “six sigmas”. Cependant la quasi-totalité des outils connus repose sur un prérequis fondamental la “Normalité” de la distribution des données mesurées. Il s’agira ici de comprendre pourquoi ce prérequis est mis en place, mais aussi de comprendre en quoi la recherche obsessionnelle de son atteinte dans le cadre d’un exercice de démonstration de maitrise et de suivi d’un procédé ne doit pas être une fin en soi.

1. La normalité et le lien avec les outils de la SPC

La loi normale, parfois aussi appelée loi de Laplace-Gauss est une loi de probabilité permettant de modéliser certains phénomènes naturels mesurables et soumis à une composante aléatoire. Dans la nature, les mesures anatomiques par exemple, suivent la plupart du temps une loi normale : pour une espèce d’êtres vivants spécifiques, la taille de la plupart des individus sera répartie de manière équilibrée autour d’une valeur moyenne même s’il existe quelques individus “hors normes”. Ce sont cette valeur moyenne (indiquant la tendance centrale des données) et cette répartition “équilibrée” de part et d’autre de la moyenne (indiquant la dispersion) qui caractérisent la loi normale.

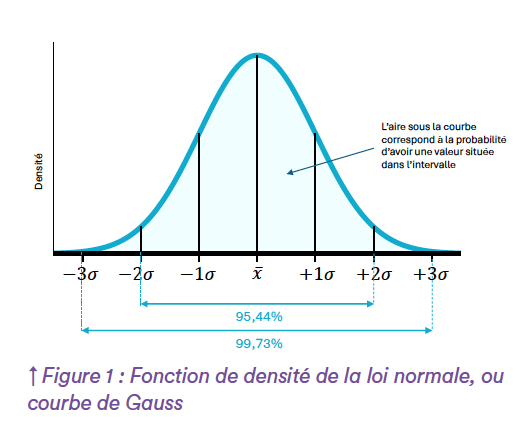
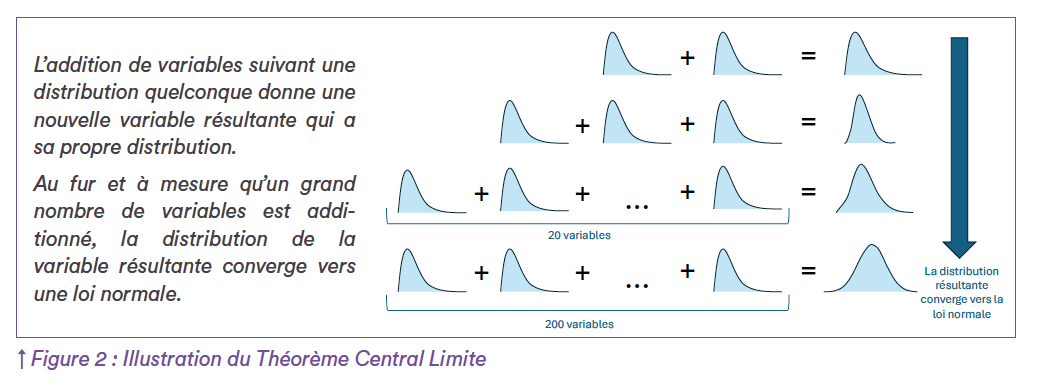
La moyenne et l’écart type permettent de représenter précisément la courbe de distribution et de pouvoir modéliser la probabilité d’apparition des différentes valeurs possibles que peuvent prendre la mesure étudiée. Une autre raison de la célébrité de la loi normale est qu’elle est une loi de convergence dans l’addition de phénomènes aléatoires. En effet, lorsqu’on étudie plusieurs phénomènes indépendants qui suivent la même distribution quelconque, le Théorème Central Limite1 montre que la somme des valeurs de ces phénomènes suit une loi normale (cf. Figure 2). De nombreux phénomènes sont dus à l’addition d’un grand nombre de petites perturbations aléatoires, d’où la prépondérance de la loi normale dans l’étude de variables quantitatives.

Cela explique pourquoi cette loi a servi de base lors du développement de l’industrialisation (Ford, Taylor, Shewart2) pour maitriser les procédés de production de masse avec le développement des méthodes de Statistical Process Control (SPC) et d’approche “six sigmas”, notamment par l’étude de mesures regroupées. La construction des outils de SPC repose sur les deux indicateurs que sont la moyenne et l’écart type qui, avec la distribution Normale, permettent de réaliser une inférence sur le positionnement global des valeurs. Lorsque la distribution est caractérisée comme étant normale, il est possible d’associer un niveau de probabilité d’occurrence à chaque plage de valeurs. Ainsi, l’étude n’est plus simplement descriptive, mais devient inférentielle : c’est-à-dire qu’il est possible de tirer des conclusions générales sur la survenue potentielle de valeurs qui n’ont pas encore été observées factuellement dans les données collectées. La carte de contrôle classique des valeurs individuelles par exemple, propose d’établir des limites de suivi permettant d’identifier des dérives. En effet, sous le présupposé de normalité, les limites construites à ± 3 de la moyenne (trois écart types de part et d’autres de la moyenne, soit “six sigmas” au total) doivent théoriquement refléter 99,73% des valeurs pouvant être prises par le phénomène étudié. La validité des règles de Nelson permettant de suivre la répartition des valeurs au fur et à mesure de la production repose, elle aussi, sur la distribution normale des données. Il en va de même pour les indices de capabilité, dont l’objectif est d’évaluer la capacité du procédé à délivrer des produits conformes aux spécifications (en termes de sécurité et d’efficacité). Pour pouvoir évaluer cette capacité, les indices de capabilités (Ppk, Cpk, Pp, Cp…) utilisent la moyenne et l’écart type des données pour les mettre en rapport vis-à-vis de la proximité ou de l’éloignement des spécifications du produit. Ainsi, les critères usuellement utilisés pour évaluer ces indices (> 1,00 , > 1,33) découlent directement de la loi normale : un Cpk ≥ 1,33 par exemple, signifie que la spécification la plus proche se situe à plus de 4 écarts-type de la moyenne, soit, selon la loi normale, moins de 0,01% de risque d’obtenir un produit hors spécification compte tenu de la distribution des données. Les différents intervalles de prévisions et de tolérance reposent, eux aussi, par construction, sur la normalité, avec la moyenne comme “valeur la plus représentative” de la distribution et l’écarttype comme “dispersion naturellement équilibrée” autour de la moyenne. Avec le présupposé de normalité, les formules associées permettent de déterminer les intervalles dans lesquels se trouveront un certain pourcentage de couverture de la population avec niveau de confiance déterminé.

2. Démontrer la normalité : les premiers écueils

Dans le cadre d’une démarche de Continued Process Verification, la problématique est de pouvoir démontrer que le phénomène étudié est en adéquation avec la distribution normale sur laquelle repose toute la logique d’établissement des outils de maitrise statistique des procédés évoqués ci-dessus. Pour ce faire, il est déjà essentiel de représenter graphiquement les données (histogramme, boxplot, droite de Henry, etc.) afin de pouvoir appréhender visuellement la forme de la distribution de l’échantillon collecté. Un écueil que l’on peut rencontrer dans cette démarche est l’utilisation de test de démonstration de la normalité. En effet, même si certains tests sont usuels (Shapiro Wilk, Anderson Darling, Kolmogorov- Smirnov, etc.), la littérature statistique ne fait pas forcément consensus sur l’utilisation d’un test en particulier. L’utilisation pertinente de ces tests nécessite une connaissance fine des enjeux statistiques en termes de caractérisation des hypothèses et de puissance attendue. Premièrement, pour choisir le test adapté, il est important d’avoir une idée a priori de la forme de la distribution alternative contre laquelle l’hypothèse de normalité sera testée, afin de maitriser la puissance du test3. La figure ci-dessous illustre ce concept : il n’y a qu’une seule façon d’être normal (H0 entièrement caractérisée), mais plusieurs possibilités d’être “non-normal”, ainsi Ha doit être supposée (cf. Figure 3). Les données peuvent s’écarter de la normalité mais rester symétriques (cas uniforme, cas de Student, cas de Cauchy, …) la problématique relève alors de la variabilité générant potentiellement des valeurs extrêmes régulièrement et on attend ici du test de Normalité qu’il soit capable de mettre ce problème en évidence. Les données peuvent aussi être non normales car présentant une asymétrie (cas d’une dérive lente par exemple) : on attend ici du test qu’il puisse également le détecter. Certains tests sont plus sensibles à la détection d’étalement de la variabilité même lorsque la symétrie est présente (Shapiro-Wilk, Lilliefors,…), d’autres seront plus performants dans la détection d’asymétrie potentielle (Anderson-Darling,…). La question est de savoir quelle distribution alternative pourrait être soupçonnée et devrait être détectée par le test, en vue d’être pertinent dans les conclusions (recherche de valeurs extrêmes ? dérive lente des données ?…). La bibliographie statistique ne fait pas complètement consensus4 sur la question du test adéquat à utiliser, même si le test de Shapiro-Wilk semble assez sensible avec différentes situations alternatives.

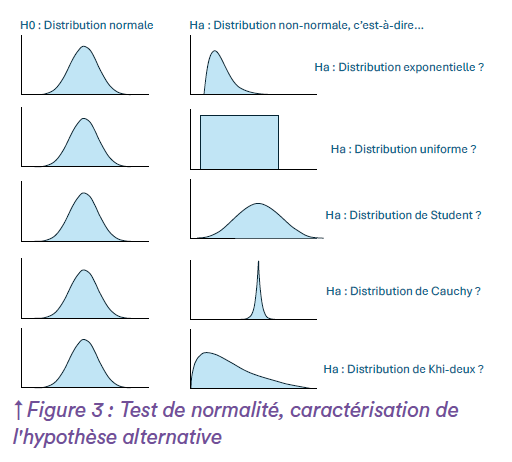
Cette caractérisation de la distribution alternative est cependant rarement étudiée en industrie pharmaceutique lorsqu’on aspire à démontrer la normalité. Le néophyte moins sensible à la méthode scientifique pourrait être tenté d’utiliser différents tests sur un même jeu de données et pourrait être confronté à des conclusions potentiellement opposées qu’il sera difficile de démêler par la suite. L’expérience de se trouver dans la situation de conclusions opposées sur la normalité nous contraint à considérer peut être à tort que le jeu de données ne suit pas une loi normale en adoptant la position la plus défavorable. Deuxièmement, le nombre de valeurs analysées (ou “taille d’échantillon”) a son importance. Les contraintes opérationnelles ne permettent pas toujours d’avoir un nombre suffisant de valeurs pour que les tests soient pertinents. En effet, avec moins de 30 valeurs, la puissance des tests classiques de normalité est faible et ils sont incapables de mettre en évidence un écart à la normalité, même lorsque celui-ci est réel. Ils amènent ainsi à conclure systématiquement à la normalité, qu’elle soit avérée ou non. Dans cette configuration, le test laisse ainsi l’expérimentateur dans le flou d’une “non significativité statistique” qui n’apporte finalement aucune réponse adaptée quant à la distribution réelle des données. Le choix du test adapté et le soin apporté aux conditions d’applications sont donc nécessaires pour pouvoir statuer sereinement sur la forme de la distribution.

3. Les causes de non-normalité : causes spécifiques vs causes naturelles

Lorsque les conditions de mise en oeuvre des tests de normalité ont été réunies, il arrive fréquemment que le test conclu néanmoins à “l’absence de normalité” des données. Tout l’enjeu ici est de comprendre le comportement de la variable étudiée en dépit de l’absence de normalité, afin d’apprécier la maitrise du procédé de fabrication dont elle est issue. Il sera donc important de disposer d’outils supplémentaires pour évaluer si “l’absence de normalité” relève d’un événement particulier qu’il faudra traiter spécifiquement, d’un comportement naturel de la grandeur étudiée ou bien d’une absence globale de maitrise du procédé. (Figure 4)

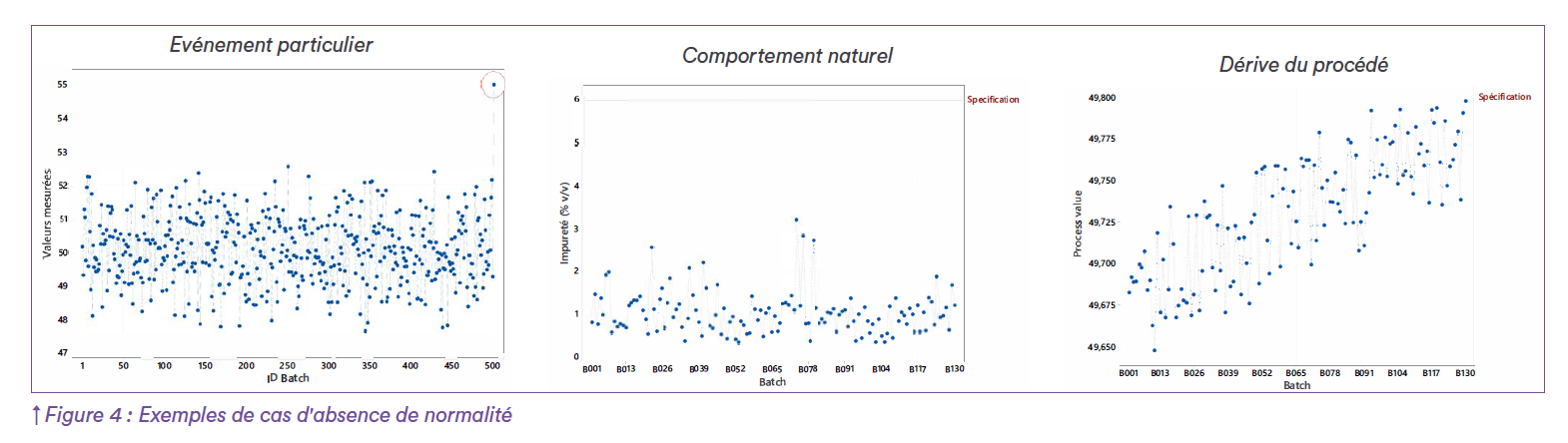
Plus largement, les outils statistiques ne sont pas des juges de paix qui érigent une vérité absolue. Ce sont des outils de compréhension et d’aide à la décision qui permettent d’appréhender des données quantitatives en y intégrant la composante aléatoire de manière méthodique. Il s’agit de contextualiser la donnée que l’on cherche à appréhender et ne pas s’en tenir à la seule p-value du test5 de manière manichéenne. Là encore, le recoupement des informations avec un expert du procédé est primordial. Ainsi, avant même les représentations graphiques et le lancement du test d’adéquation à la normalité, l’expérimentateur doit idéalement avoir une idée a priori du phénomène qu’il est en train d’étudier. Par exemple, en présence d’une variable pilotée par un procédé et centrée autour d’une valeur cible, qui devrait se distribuer normalement, tout échec au test de normalité doit amener à s’interroger sur de possibles perturbations dans l’échantillon observé. Dans cette perspective, les représentations graphiques (histogramme, boxplot, droite de Henry, etc.) seront d’un grand secours pour identifier la marche à suivre et comprendre le résultat du test. En effet, la normalité peut être rejetée pour des causes très différentes qui appellent des stratégies d’approche adaptées. Dans le cas d’échec de la normalité lié à la présence d’une ou plusieurs valeurs aberrantes, il s’agira d’identifier les causes potentielles de ces valeurs et de s’assurer qu’elles résultent d’événements spécifiques pouvant être mis sous contrôle (erreur de manipulation, défaut de mesure, etc.) et non pas de la variabilité du procédé. (Figure 5) Si une cause de l’obtention de cette valeur extrême peut être identifiée et peut être évitée à l’avenir par une correction adaptée, il est possible de supprimer cette valeur de l’étude statistique et de poursuivre l’analyse de la distribution. Dans le cas contraire, si aucune cause n’est trouvée, la valeur relève peut être d’une variabilité qui n’est pas sous contrôle et qui peut se réitérer. Dans ce cas il faut la conserver dans l’analyse statistique afin de ne pas minimiser artificiellement la variabilité du procédé. Les conditions de collecte des données ont également leur importance. Lorsque la variable étudiée est mesurée en fin de ligne par exemple, elle peut regrouper plusieurs sous-populations issues de machines dont les réglages sont légèrement différents. La Figure 6 montre la distribution des données de poids mesurées après la répartition de produits dans des flacons. En haut, la distribution globale est “trop étalée” sur les valeurs centrales pour s’accorder avec la normalité, c’est pourquoi le test conclu à l’absence de normalité. En effet, les données finales résultent de deux pompes de répartition dont les tendances centrales sont légèrement décalées. La figure du bas montre les distributions valeurs scindées pour chacun des équipements. Il s’agira alors d’évaluer l’impact de ce décalage (réglage machine à réitérer ?) et/ou de déplacer le point de contrôle (sortie de pompe) selon les besoins opérationnels. Les moyens de collecte de la donnée sont également à prendre en compte lorsqu’on étudie un phénomène. Parfois, la méthode d’analyse ou la résolution de l’équipement de mesure ne permettent pas d’obtenir un nombre de décimales permettant de révéler toute la variabilité fine du phénomène étudié. La distribution obtenue contient donc un artéfact lié à l’arrondi et générant de nombreuses valeurs ex-aequo qui peuvent conduire à l’échec du test de normalité. La Figure 7 illustre ce phénomène, à gauche des valeurs ont été simulées selon une distribution normale pour exprimer théoriquement le potentiel Hydrogène réel d’une solution. A droite, les mêmes données ont été arrondies au dixième pour exprimer ces mêmes valeurs de pH mesurées avec un pH-mètre permettant d’obtenir des mesures seulement au dixième. A gauche, le test d’Anderson-Darling ne rejette pas la normalité, alors qu’à droite il la rejette par manque de “variabilité” liée à la faible résolution de l’équipement de mesure. Là encore, cette configuration doit être anticipée par la connaissance métier, qui peut préférer gérer ces artéfacts en amont en choisissant d’évaluer ce type de paramètres via un test statistique adapté à cette problématique, comme le test d’Agostino6 par exemple qui est peu sensible aux valeurs ex-aequo.

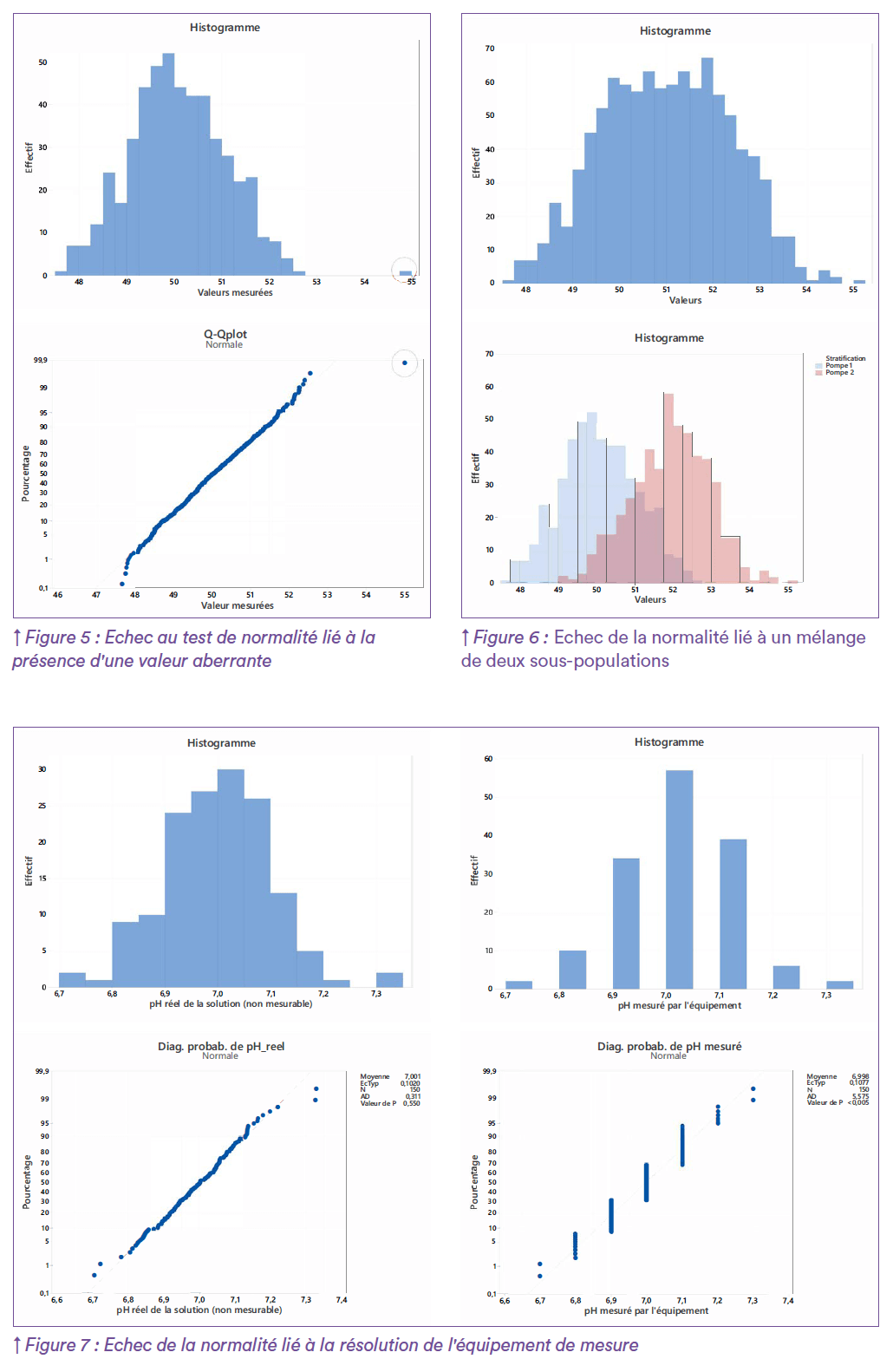
Le Tableau 1 ci-après montre l’analyse de la distribution de la variable “pH mesuré” (Figure 7) avec différents tests statistiques. Seul le test d’Agostino n’est pas influencé par les valeurs ex-aequo et sa conclusion concorde avec la simulation originale. Les distributions des données étudiées peuvent parfois présenter une asymétrie qui correspond à la nature même du phénomène. C’est le cas par exemple lorsque l’on suit des durées de process (Figure 8) : la plupart des temps peuvent être courts et limités en valeur basse en raison des durées minimales d’étapes et s’allonger pour des causes précises liées à la vie habituelle du procédé. Ce type de variable ne peut pas suivre une distribution normale par nature et présente une asymétrique par essence. Dans une démarche CPV, ce type d’asymétrie dans la distribution est fréquente compte tenu du type des produits pharmaceutiques (e.g. humidité résiduelle des poudres et lyophilisats, taux d’impuretés, …) ou des étapes de transformation de la matière (e.g. rendements). Les variables relatives aux produits et intermédiaires type “impuretés” talonnent généralement sur une valeur faible et présentent de manière ponctuelle quelques valeurs plus élevées. Dans l’autre sens, les variables relatives au procédé telles que des rendements peuvent présenter une distribution asymétrique à gauche : une majorité des valeurs talonnent le 100% alors que la distribution s’étire vers des valeurs plus faibles. C’est ce type de phénomène qu’il est important d’identifier, car dans ce cas, la moyenne n’est plus un indicateur représentatif de la tendance centrale. La variabilité n’est plus répartie de manière équilibrée autour de la moyenne (l’écart-type n’est plus un indicateur adapté à l’évaluation de la dispersion). Ici typiquement, tous les outils liés au “six sigmas” (cartes de contrôle avec limites à ±3 , calcul classique des indicateurs de capabilités, etc.) perdent totalement leur pertinence et ne sont pas applicables. Pour autant, la maîtrise du procédé et sa démonstration restent soutenables.

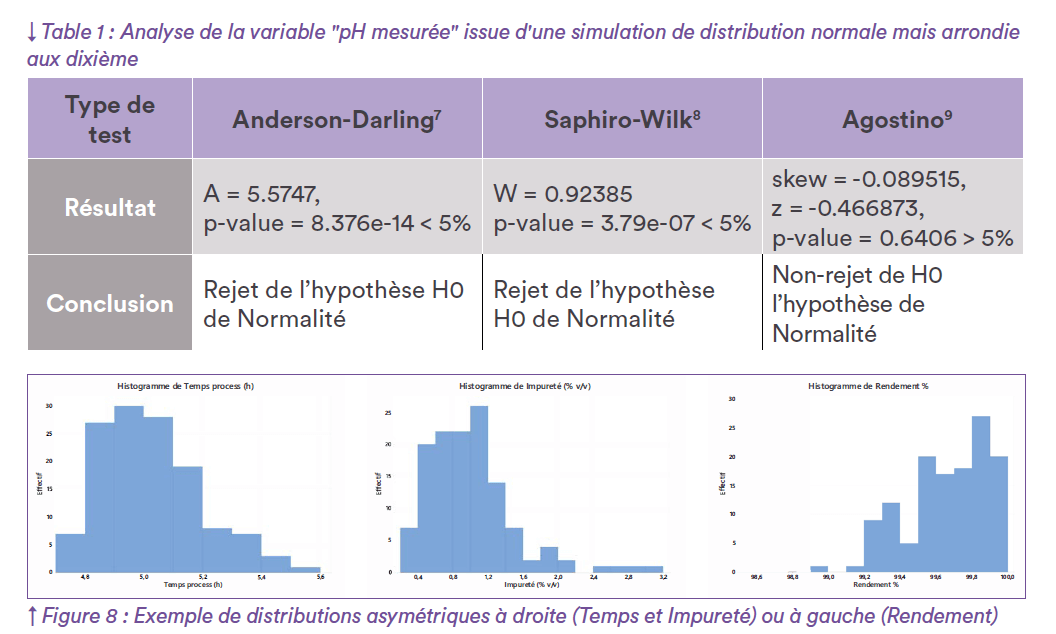
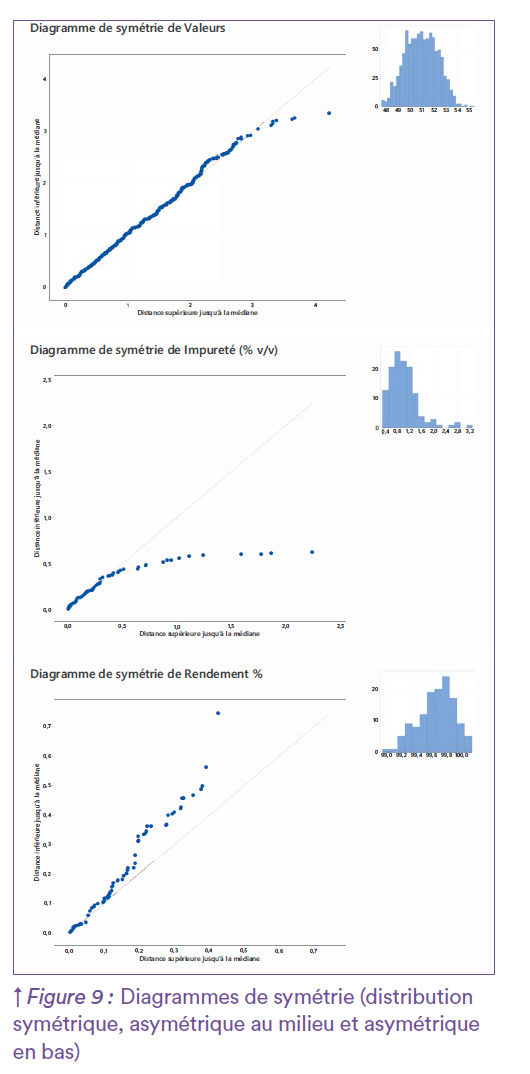
4. Normalité et mise sous contrôle : deux concepts à ne pas confondre en Continued Process Verification

Mettre sous contrôle un procédé de fabrication pour assurer la qualité d’un produit nécessite de ne pas perdre de vue l’objectif et de ne pas confondre le moyen et la finalité. En effet, la normalité d’une distribution est un prérequis à l’utilisation d’outils statistiques facilement applicables, c’est-à-dire un moyen de poursuivre une analyse. Cependant, la normalité n’est pas un prérequis pour assurer la maitrise du procédé en ellemême. De ce fait, l’absence de normalité n’implique pas nécessairement une absence de maitrise en Continued Process Verification. Tout l’enjeu est de pouvoir détecter les situations relevant de sources de variations spéciales nécessitant la mise en place d’une amélioration, de celles relevant de sources de variation “communes” , qui font partie de la vie habituelle du procédé et qui doivent être évidemment compatibles avec les requis qualité et sécurité du produit. Ainsi, un procédé peut être sous contrôle même lorsque la normalité d’un paramètre de suivi n’est pas vérifiée, notamment si l’absence de normalité est liée à l’essence des données (Figure 8) ou à la résolution du moyen de mesure (Figure 7). Dans toutes ces situations, il faudra alors utiliser des outils d’analyse statistique adaptés à l’évaluation des données, afin de pouvoir statuer sur la maitrise du procédé sans toutefois tomber dans des écueils méthodologiques qui rendraient l’étude inconsistante. Lorsque le moyen de mesure ne permet pas d’obtenir des valeurs avec une résolution adaptée à la faisabilité d’un test de normalité, mais que la connaissance métier permet d’être théoriquement confiant sur la stabilité du paramètre, il peut être pertinent de contourner l’artefact de mesure par l’étude de la symétrie et de l’étalement de la distribution. Prenons en exemple un paramètre présentant de nombreuses valeurs ex-aequo (faisant échouer le test de normalité) mais affichant une distribution dont les valeurs ciblent une même tendance avec une répartition équilibrée autour de celle-ci. Ici, l’analyse préalable de la distribution nécessitera de s’assurer de la symétrie réelle de la distribution avec un mode central, en utilisant par exemple les coefficients de Skewness (asymétrie) et de Kurtosis (aplatissement) ou des diagrammes de symétrie (voir Figure 9). Dans cette perspective, il pourrait être adapté de continuer à utiliser les outils classiques (carte de contrôle avec limites à ±3 , indices de capabilité, etc.), dans la mesure où conceptuellement, on attend aussi ici du procédé qu’il délivre des produits dont les valeurs se répartissent autour d’une cible et que l’industriel souhaite être alerté si cette situation dérive. La démarche de démonstration de maitrise du procédé se complexifie lorsque le paramètre étudié semble suivre une loi différente de la loi normale. A nouveau, le travail en interdisciplinarité sera ici primordial dans le cadre du processus de CPV pour discriminer entre “cause spéciale” et “cause commune”. Les causes spéciales doivent bien sûr faire l’objet d’une amélioration du procédé. En revanche lorsque la cause est commune (le paramètre suit une autre loi par essence), plusieurs approches son  possibles. La bibliographie statistique regorge d’exemples de transformations normalisantes10 permettant de replacer la distribution des données transformées dans la situation de normalité et donnant l’espoir de pouvoir reprendre l’analyse à l’aide des outils statistiques usuels. Les difficulté  ne sont pas pour autant évacuées puisque le choix de la transformation devra être opéré (transformation polynomiale  transformation de Johnson, transformation de Box-Cox, etc.) et justifié (suivi dans le cadre de décisions pharmaceutiques)  Une fois les transformations réalisées et la normalité retrouvée, il faut pouvoir ensuite répondre à l’objectif initial de démonstration de maitrise. Le but est de pouvoir proposer des limites de suivi de la tendance et de la variabilité du procédé en grandeurs physiques qui soient accessibles aux expertises métiers et qui puissent être interprétables dans l’unité des données initiales. Selon la complexité de la transformation, il ne sera pas toujours possible de revenir au domaine de la grandeur physique par une transformation inverse et ainsi, l’objectif de démontrer la maitrise du procédé et de mettre en place un suivi aura totalement échoué.

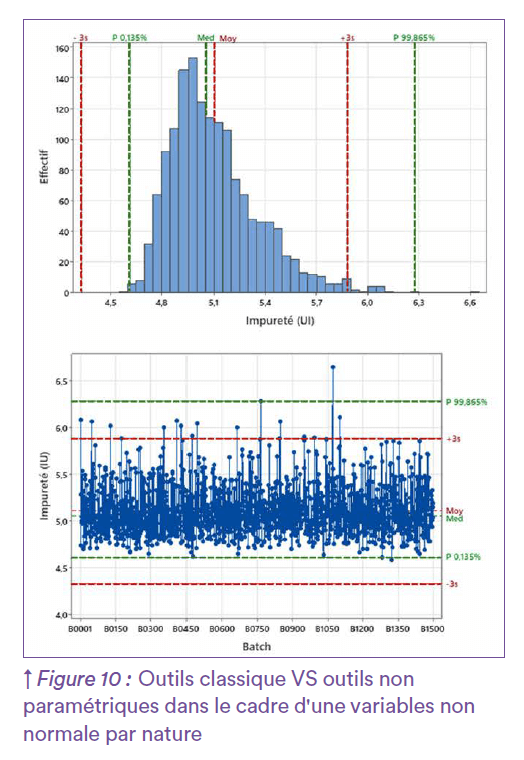
Une autre approche serait de s’affranchir définitivement de la normalité en se raccrochant aux propriétés de la distribution intrinsèque des données. Il s’agira alors d’assumer une posture épistémologique à savoir : soit amorcer l’étude d’un point de vue empiriste par essai/erreur à partir des données observées, soit entreprendre une démarche rationaliste qui devra s’appuyer sur l’état des connaissances scientifiques afin de remplir, de manière pertinente, l’objectif de démonstration de maitrise du procédé. L’approche empiriste consiste à identifier la loi de distribution en évaluant l’adéquation des données observées vis-à-vis d’un casting de lois candidates théoriques. De nombreux tests statistiques “d’adéquation à une distribution” permettent de réaliser cette évaluation. Lorsque plusieurs lois candidates répondent positivement à l’adéquation, la problématique sera de pouvoir faire un choix, sachant que les impacts sur les indicateurs de maitrise du procédé pourront être très divers selon la loi retenue. L’approche rationaliste, quant à elle, serait de s’appuyer sur l’état des connaissances scientifiques du paramètre étudié (modèle biologique, loi connue de par ailleurs -type Weibull par exemple-,…). L’adéquation à la loi théorique peut également être vérifiée au préalable et le fait que cette loi soit caractérisée permet de transposer les concepts du “six sigmas” sur la nouvelle distribution. Par exemple pour les limites de suivi, elles peuvent être définies par les quantiles théoriques de la loi correspondant à une probabilité de 99,73%. La capabilité peut aussi être évaluée théoriquement à partir de la loi scientifique en évaluant la probabilité qu’une variable suivant cette loi théorique dépasse un seuil de spécification défini, grâce à des méthodes d’intégration numérique. Les indices de capabilité (Pp, Ppk) peuvent être recalculés via cette nouvelle loi et leur seuils d’évaluation maintenus (> 1,00 ou > 1,33) avec la même dimension interprétative et inférentielle. Néanmoins, pour réaliser cette démarche, il faut avoir un état des connaissances scientifiques suffisamment riche pour utiliser la loi théorique et décliner toute l’approche SPC sur cette nouvelle base. En pratique cet état de connaissances scientifique est rarement accessible. Dans une perspective plus modeste, il est également possible d’utiliser des outils non-paramétriques ou “distributions free”11 qui ne font aucun présupposé sur la forme de la distribution et permettent de rendre compte synthétiquement de ce qui a été observé sur les données. L’idée ici est de s’appuyer sur les percentiles observés (0,135% et 99,865%) pour se ramener dans le cadre conceptuel de ce qui est réalisé avec les outils de SPC dits “classiques”. Il est alors possible de construire des limites de suivi et des indicateurs de capabilité non-paramétriques à partir du jeu de données collecté. Cependant, l’étude délivre des conclusions purement descriptives qui font état des lieux de la variabilité du procédé sur le moment, et ne permettent pas de faire de l’inférence quant aux valeurs futures qui seront générées, ni de prétendre à une prévision probabiliste de la maitrise du procédé. Ces outils permettent néanmoins d’initier un suivi en l’absence de distribution caractérisée et d’avoir un premier retour sur le niveau de maitrise du procédé. La Figure 10 permet de comparer cette approche non-paramétrique sur une distribution asymétrique par nature versus l’utilisation d’outils classiques qui seraient un écueil méthodologique. L’utilisation automatique d’outils classiques (en rouge) est inappropriée : la moyenne et les limites à ± 3 écarts types ne traduisent pas la distribution de la population. En revanche, les outils non-paramétriques (en vert) permettent d’obtenir des limites qui reflètent l’asymétrie de la distribution tout en discriminant les points usuels des points plus extrêmes qu’il faudra étudier spécifiquement. A défaut d’être sophistiqués, les outils non-paramétriques permettent de mettre en place un suivi opérationnel de la maitrise du procédé, suivi qui sera adapté à la distribution des données.

Conclusion

En définitive, démontrer la maitrise d’un procédé dans le contexte de la CPV nécessite de s’appuyer sur une vue d’ensemble des connaissances scientifiques. Les outils statistiques sont un support pour résumer l’information portée par les données de manière méthodique. Cependant ils doivent être utilisés à bon escient. En effet, il est important de ne pas s’enfermer dans les outils mais de toujours recontextualiser les données, leur interprétation et les conclusions. La distribution “normale” doit simplement rester un prérequis à l’utilisation d’outils plus simples et plus fréquemment usités mais ne doit pas être un objectif en soi. La maitrise du procédé dans un exercice de Continued Process Verification doit résulter d’une mise en lien des connaissances entre les différentes expertises scientifiques (produit, procédé, analytique,…) qui peuvent guider l’utilisation d’outils statistiques parfois singuliers mais dont la pertinence sera mieux adaptée à l’objectif.

Références

1. Pierre-Simon Laplace, “M.moire sur les approximations des formules qui sont fonctions de très-grands nombres, et sur leur application aux probabilités”, M.moires de la Classe des sciences mathématiques et physiques de l’Institut de France, 1809, p. 353-41

2. Shewhart, W.A. (1931). Economic Control of Quality of Manufactured Product. American Society for Quality Control.

3. Razali, N. and Wah, Y. (2011) Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. Journal of Statistical Modeling and Analytics, 2, 21-33.

4. Arnastauskaite, J., Ruzgas, T., & Braženas, M. (2021). An Exhaustive Power Comparison of Normality Tests. Mathematics, 9(7), 788. https://doi.org/10.3390/math9070788

5. Amrhein, V., Greenland, S., & McShane, B. (2019). Scientists rise up against statistical significance. Nature, 567(7748), 305–307. https://doi.org/10.1038/d41586-019-00857-9

6. D’Agostino, R.B. (1986), Tests for the Normal Distribution, in D’Agostino, R.B. and Stephens, M.A. (eds.), Goodness-of-fit Techniques (pp. 367-419). New York: Marcel Dekker.

7. Réalisé sous R avec le package {nortest} version 1.0-4

8. Réalisé sous R avec le package {stats} version 4.1.1

9. Réalisé sous R avec le package {moments} version 0.14.1

10. Daumas, F. (1982). Méthodes de normalisation des données. Revue de statistique appliquée, 30(4), 23-38.

11. Potvin, C., & Roff, D. A. (1993). Distribution-Free and Robust Statistical Methods: Viable Alternatives to Parametric Statistics. Ecology, 74(6), 1617–1628. https://doi.org/10.2307/1939920

Partager l’article

Michel HERTSCHUH

Voir le profil sur

Mannaïg MACUMI

Voir le profil sur